Hari/Tanggal : Jumat, 23 Mei 2025
Mata Pelajaran : Matematika Bangun Ruang
Alat Peraga : Video Pembelajaran
Metode Pembelajaran : Diskusi dan Tanya Jawab
Good morning my lovely students. How are you this morning?
Matematika
Elemen CP : Pada akhir Fase B, peserta didik dapat mengukur panjang dan berat benda menggunakan satuan baku. Mereka dapat menentukan hubungan antar-satuan baku panjang (cm, m). Mereka dapat mengukur dan mengestimasi luas dan volume menggunakan satuan tidak baku dan satuan baku berupa bilangan cacah.
Tujuan Pembelajaran :
1. Peserta didik mampu menentukan panjang benda dengan tepat dengan bangun ruang
Alur Tujuan Pembelajaran :
1. Peserta didik mengukur panjang dengan bangun ruang menggunakan satuan baku.
Materi Pembelajaran
Apa itu Bangun Ruang?
Bangun ruang adalah bentuk yang memiliki panjang, lebar, dan tinggi. Bangun ruang berbeda dengan bangun datar yang hanya memiliki panjang dan lebar aja. Bangun ruang berbentuk tiga dimensi (3D), sementara bangun datar berbentuk dua dimensi (2D).
Pada bangun ruang, kita bisa mencari luas permukaan dan volume. Wah, apa itu volume? Volume adalah kapasitas atau penghitungan seberapa banyak ruang yang bisa ditempati/diisi oleh suatu objek.
Misalnya seperti saat kita mengisi botol air minum. Biasanya kan, botol air minum memiliki ukuran kapasitas yang tertera di bagian bawah botol, seperti 500 ml, 700 ml, atau 1 liter. Nah, kapasitas inilah yang dinamakan volume. Jika suatu botol air minum tertulis memiliki volume 1 liter, maka jumlah maksimal air minum yang dapat ditampung oleh botol tersebut adalah sebanyak 1 liter.
Ciri-Ciri Bangun Ruang
Secara umum, ciri-ciri atau sifat-sifat bangun ruang adalah sebagai berikut:
- Memiliki wajah atau sisi permukaan
- Memiliki tepi atau rusuk (tempat bertemunya sisi dengan sisi lainnya)
- Memiliki sudut
- Memiliki volume
Ciri yang disebut di atas juga dapat disebut sebagai unsur-unsur bangun ruang, atau karakteristik yang harus dimiliki suatu bangun untuk dapat disebut sebagai bangun ruang.
Rumus Luas dan Volume Bangun Ruang
1. Rumus Luas dan Volume Kubus
Kubus adalah bangun ruang yang memiliki enam sisi berbentuk persegi yang sama besar. Semua rusuk pada kubus memiliki panjang yang sama.
Ciri-Ciri Kubus
- Memiliki 12 rusuk yang panjang sama.
- Memiliki 6 sisi berbentuk persegi.
- Memiliki 8 titik sudut.
- Memiliki 12 diagonal sisi atau diagonal bidang.
- Memiliki 4 diagonal ruang.
- Memiliki 6 bidang diagonal.
- Memiliki 3 pasang bidang sejajar yang sama dan sebangun.
Rumus Luas Permukaan Kubus
Luas Permukaan = 6 × sisi × sisi
L = 6 × s2
Rumus Volume Kubus
Volume = sisi × sisi × sisi
V = s3
Contoh Soal:
Sebuah kubus memiliki panjang sisi 4 cm. Hitunglah luas permukaan dan volumenya!
Pembahasan:
Diketahui: s = 4 cm
Ditanya: L dan V …?
Jawab:
a. Luas permukaan kubus
L = 6 × s2
L = 6 × 42
L = 6 × 16 = 96 cm²
Jadi, luas permukaan kubus tersebut adalah 96 cm².
b. Volume kubus
V = s3
V = 43
V = 64 cm³
Jadi, volume kubus tersebut adalah 64 cm³.
2. Rumus Luas dan Volume Balok
Sama seperti kubus, balok adalah bangun ruang yang memiliki enam sisi, namun sisi-sisinya berbentuk persegi panjang. Tiga pasang sisi balok yang berhadapan akan sama besar.
Ciri-Ciri Balok
- Memiliki 6 buah sisi.
- Memiliki 12 rusuk.
- Memiliki 12 diagonal bidang.
- Memiliki 8 titik sudut.
- Memiliki 4 diagonal ruang.
- Memiliki 6 bidang diagonal.
- Memiliki luas permukaan dan volume.
Rumus Luas Permukaan Balok
Luas Permukaan = 2 × ((panjang × lebar) + (panjang × tinggi) + (lebar × tinggi))
L = 2 × ((p × l) + (p × t) + (l × t))
Rumus Volume Balok
Volume = panjang × lebar × tinggi
V = p × l × t
Contoh Soal:
Sebuah balok memiliki panjang 8 cm, lebar 4 cm, dan tinggi 6 cm. Hitunglah luas permukaan dan volumenya!
Pembahasan:
Diketahui: p = 8 cm, l = 4 cm, t = 6 cm
Ditanya: L dan V …?
Jawab:
a. Luas permukaan balok
L = 2 × ((p × l) + (p × t) + (l × t))
L = 2 × ((8 × 4) + (8 × 6) + (4 × 6))
L = 2 × (32 + 48 + 24) = 208 cm²
Jadi, luas permukaan balok tersebut adalah 208 cm².
b. Volume balok
V = p × l × t
V = 8 × 4 × 6 = 192 cm³
Jadi, volume balok tersebut adalah 192 cm³.
3. Rumus Luas dan Volume Limas
Selanjutnya, limas adalah bangun ruang yang memiliki alas berbentuk segitiga, segiempat, segilima, segienam, dan seterusnya (segi-n), dan sisi-sisi tegak berbentuk segitiga yang bertemu di satu titik puncak.
Jika alas limas berbentuk segitiga, maka bangun tersebut disebut limas segitiga. Jika alasnya berbentuk segiempat, maka disebut limas segiempat, begitupun dengan limas segilima, limas segienam, dan seterusnya.
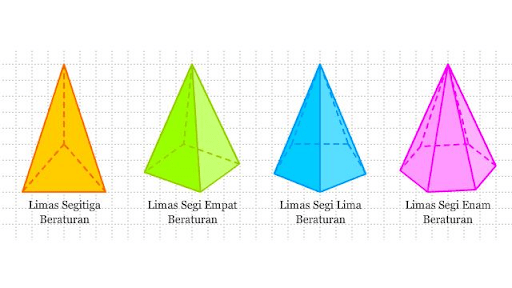
Ciri-Ciri Limas
- Memiliki 7 titik sudut.
- Memiliki 12 rusuk.
- Memiliki 6 sisi tegak.
- Memiliki 1 sisi alas.
- Mempunyai sisi tegak berbentuk segitiga.
- Sisi alasnya berbentuk segi banyak.
- Mempunyai satu titik puncak.
- Penamaan limas tergantung bentuk alasnya.
Rumus Luas Permukaan Limas
Luas Permukaan = Luas alas + Luas selimut
L = Lalas + Lselimut
Rumus Volume Limas
Volume = 1/3 × Luas alas × tinggi limas
V = 1/3 × Lalas × t
Keterangan:
- Luas alas limas, rumusnya tergantung pada bentuk alas limas. Misalnya, pada limas segiempat, luas alasnya = p x l.
- Luas selimut adalah luas sisi-sisi tegak limas. Karena sisi-sisi tegak limas berbentuk segitiga, maka Lselimut = 1/3 × panjang alas × t.
Contoh Soal:
Sebuah limas persegi memiliki panjang sisi alas 5 cm dan tinggi 10 cm. Hitunglah luas permukaan dan volumenya!
Pembahasan:
Diketahui:
p = 5 cm
t = 10 cm
Ditanya: L dan V …?
Jawab:
a. Luas permukaan limas
L = Lalas + Lselimut
Kita cari luas alas dan luas selimutnya satu per satu, ya!
- Luas alas
Karena alas limas tersebut berbentuk persegi, jadi untuk mencari luas alas, kita menggunakan rumus mencari luas persegi.
L = s2 = 52 = 25 cm²
- Luas selimut
Kemudian, untuk luas selimut, kita bisa gunakan luas segitiga, yaitu:
L = ½ × a × t
L = ½ × 5 × 10 = 25 cm²
Setelah kita mendapatkan luas alas dan luas selimutnya, barulah kita bisa mencari luas permukaan limas.
L = Lalas + Lselimut
L = 25 + 25 = 50 cm²
Jadi, didapat luas permukaan limas persegi tersebut adalah 50 cm².
b. Volume limas
V = 1/3 × Lalas × t
V = 1/3 × 25 × 10 = 83,33 cm³
Jadi, volume limas persegi tersebut adalah 83,33 cm³.
Baiklah itu saja materi pembelajaran kita hari ini, semoga ananda solih soliha bu guru dapat memahami materi dengan baik. Jangan lupa tetap semangat dalam belajar dan selalu melaksanakan sholat 5 waktunya ya nak.




0 komentar:
Posting Komentar